ycdxsb papers / security / automatic_analyse21 分钟 读完 (大约 3115 个字)  0次访问

Similarity of Binaries Across Optimization Levels and Obfuscation(ESORICS 2020)

现有的二进制相似度检测工作并没有很好的解决编译优化和混淆带来的影响，所以作者提出了IMOPT来重新优化代码，用于提高代码相似性检测的准确率。

该方法在测试集上和原本的Asm2vec相比，将精度提高了22.7%，并且可以缓解ollvm混淆带来的影响

Introduction#

现有工作的不足：

  • 静态方法：只统计静态特征，很难揭示语义特征
  • 动态方法：一旦加入混淆，junk code等会严重影响代码相似性检测

所以作者提出了IMOPT方法，通过re-optimize lifted binary缓解编译优化和混淆对代码相似性检测的影响，提高准确率。

由于作者是在二进制上进行这项工作，因此不得不面对下面两个主要的挑战：

  • 挑战1：对二进制代码的优化需要准确的指针分析，然而编译过程删除了很多变量信息。即使是编译器，在做指针分析时，也会出错：例如对于下面的代码，不优化时会输出0，而使用O2优化时，会输出1(这是真的，我帮大家试过了)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#include<stdio.h>

int confound_compiler_opt(){
    int a,b,*c;
    if(&b > &a) c = &b-1;
    else c = &b+1;
    *c = 11;
    a = 10;
    return *c - a;
}

int main(){
    int i = confound_compiler_opt();
    printf("%d\n",i);
}
  • 挑战2：在指针分析中需要对成本和精度进行折中考虑。

对于上面的两个挑战，作者也在文中提出了相应的解决方案：

  • 对于挑战1：集成精确的指针分析框架，并实现了canonicalization和elimination两类优化，这两类对相似性比较的影响最大。

    canonicalization：将逻辑上等价的表达式转换成统一形式

    elimination：通过可达性分析删除无用或不可达的代码

  • **对于挑战2：**提出了immediate SSA(static single-assignment) transforming algorithm（立即的SSA转换算法），将变量或指针即时的转换为SSA形式。采用SSA，是速度和精确度权衡的结果

主要贡献：

  • immediate SSA，O(1)复杂度的快速准确的指针分析
  • 指针分析框架
  • 二进制代码重优化方法
  • IMOPT实现

基本概念#

SSA#

静态单赋值：

1
2
3
4
x = 1;                         x1 = 1;
y = 2; 						==>          y1 = 2;
x = x - y;                     x2 = x1 - y1;
y = x + y;                     y2 = x2 + y1;

好处是一个use只有一个def，方便做def-use分析。同名变量有相同的值，变量的使用只有唯一的定义

Dominator#

控制节点：

n dominates m (n dom m) ：从entry节点到m的所有路径都需要经过节点n，称n是m的dominator

Dominance Frontier#

Dominance Frontier表示控制流图中聚合的点

对于图节点N，DF(N)是一个集合，该集合包含Z，如果Z满足：

  • N是Z某个前驱节点的控制节点
  • N不是Z的控制节点

即$DF(N) = {Z | (\exists p \in Pred(Z)) N \ dom \ p \land !N \ dom\ Z }$

这个东西可以用来实现最小SSA，并引入PHI节点。例如通过下面的控制流图

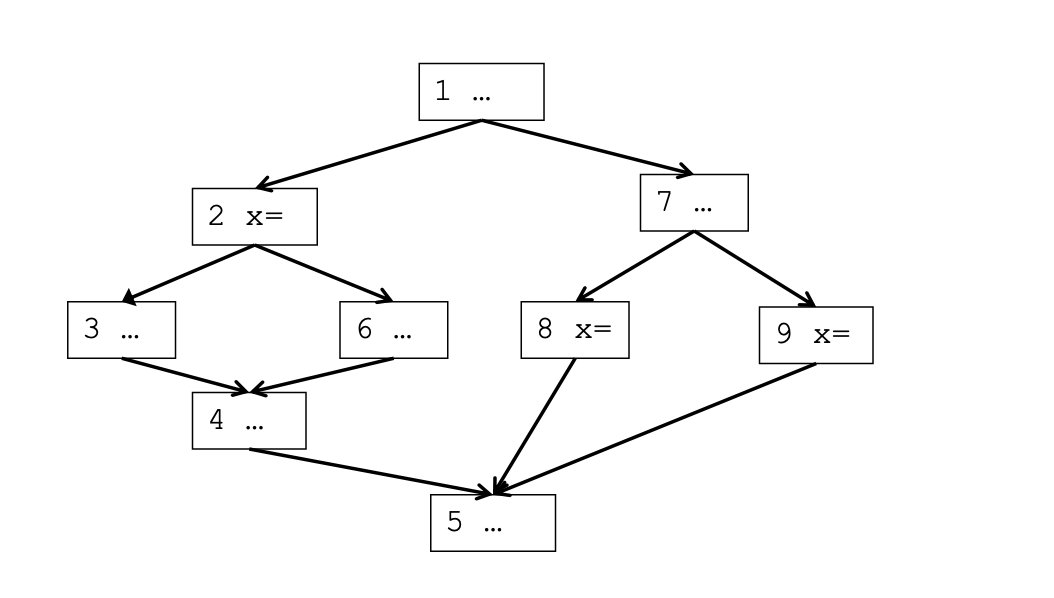
image-20201124113007402

我们可以得到Dominance Frontier如下

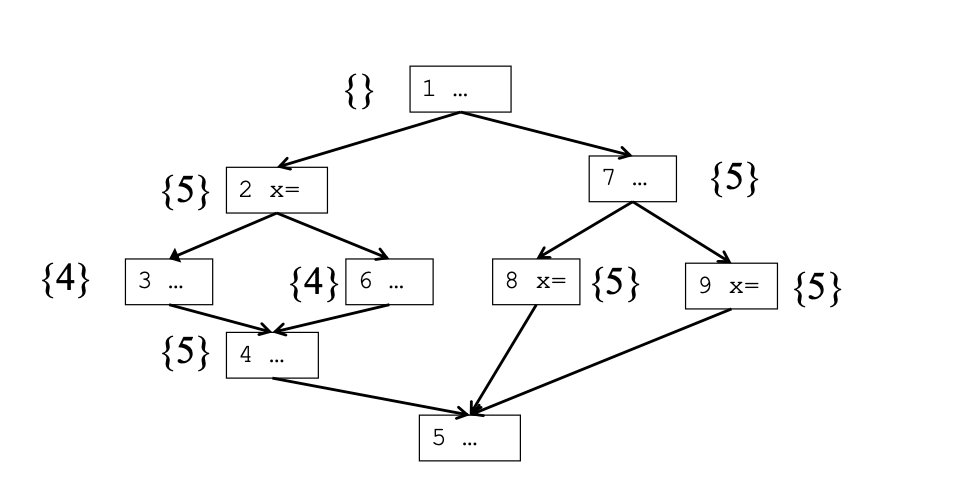
image-20201124113410026

即块2和块8和块9中的对变量x的定义会在块5处聚合。

PHI function#

为了引入最小SSA，需要利用Dominance Frontier加入PHI节点，示例如下

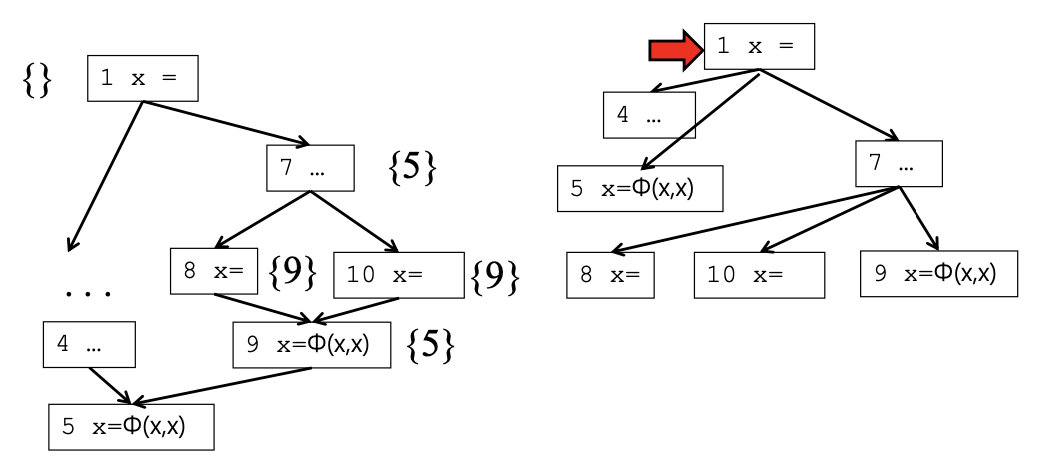
image-20201124113904892

对于左侧示例，我们可以得到Dominance Frontier并在聚合处加入PHI节点

一些术语#

  • 前向块(Forward Block)，后向块(Backward Block)，回边(Back edge)：如果有a dom b，那么边a->b 叫做回边，回边指向的块为后向块，其余都是前向块

  • 前向定义(Forward Definition)，后向定义Backward Defination：回边起点如果存在对回边终点的变量定义，则为后向定义，否则为前向定义

  • 反向可达图(Backward reachable graph)：感觉就是CFG，然后将边反向

即时性#

即时性是动态地将代码转换成SSA形式并有效维护信息的关键。

如果算法在处理时满足下面两个不变量，那么该算法具有即时性：

  • 全局不变性：处理一个基本块前，对于块中每个变量v：1)如果只有一个def可以到达该基本块，且基本块前无PHI节点，应记录v的下标；2)否则，应该插入PHI节点，且PHI节点中下标应与其他def下标不同。
  • 局部不变性：处理一个基本块后，这个基本块中使用的变量只能存在一个def点可以到达use点，且下标需要一致 。

全局不变性确保每个传入的定义都被记录，且插入必要的PHI节点

局部不变性确保每个use都与def关联

这两点也保证了SSA的正确性

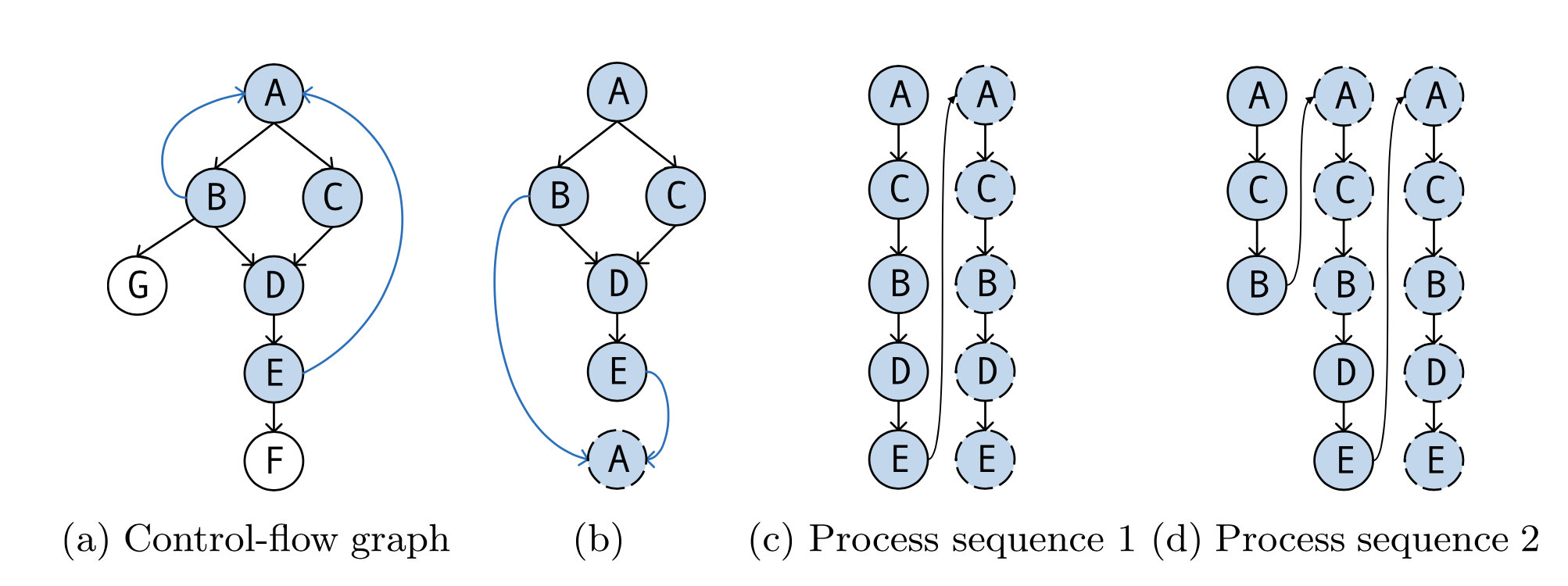
**演绎条件(Condition 1) **：算法在CFG的逆后续(Reverse post-order)遍历中进行，在处理块i前，保证每个已处理的块j都满足即时性(j<i)

逆后续遍历：

1
2
3
4
5
6
7
8
9
10
11
12
def postorder(graph, root):
    """Return a post-order ordering of nodes in the graph."""
    visited = set()
    order = []
    def dfs_walk(node):
        visited.add(node)
        for succ in graph.successors(node):
            if not succ in visited:
                dfs_walk(succ)
        order.append(node)
    dfs_walk(root)
    return order
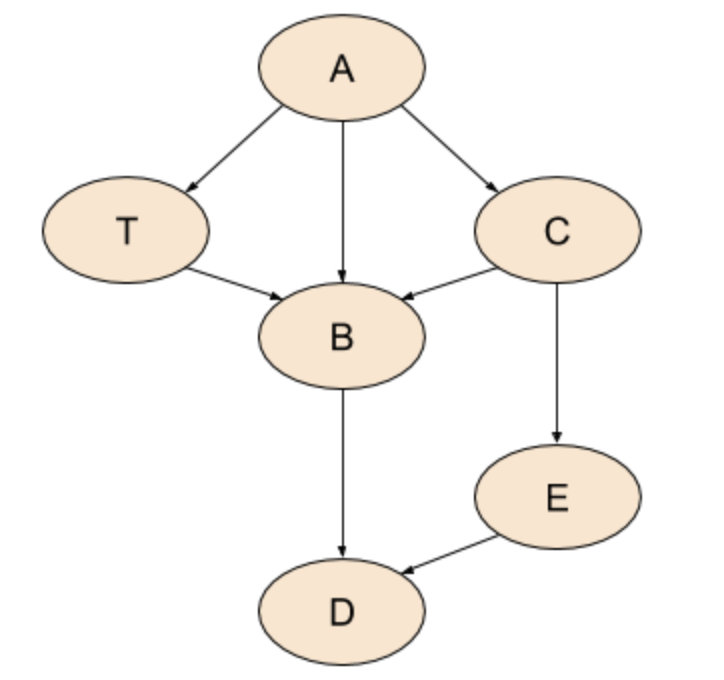
image-20201124143708676

对于上述示例，有：

  • Pre-order: A, C, B, D, E, T
  • Post-order: D, B, E, C, T, A
  • Reverse-post-order(RPO): A, T, C, E, B, D

示例结果不太符合我们习惯，比如是逆时针访问还是按字母顺序访问，简单来说逆后续遍历就是后续遍历的反向。在SSA图中，这样保证了在处理时use肯定在def后

一些引理#

Symbols B, D, S, V are used to represent the set of blocks, definitions, statements and variables.

image-20201124144805085

IMSSA 算法#

主函数#

在实现IMSSA算法时，会维护下列信息

Symbols B, D, S, V are used to represent the set of blocks, definitions, statements and variables.

image-20201124152513302

即def-use边，可达边，Dominating def，最大SSA下标数。

算法按照RPO顺序对函数进行处理，如下

image-20201124152646888

主函数十分简洁明了，不需要过多解释

找SSA的use和def点#

补充：

1
2
RHS: 赋值操作的右侧，例如 x = y + z中的 y 和 z
LHS: 赋值操作的左侧，例如 x = y + z中的 x

是正常的SSA生成的算法，不是新方法

image-20201124153537218

  1. IF:s是一个phi函数，且s属于基本块bi，遍历所有可以到达bi的块bj，修改块bjRHS中对变量v使用的下标
  2. ELSE:否则，修改bi中RHS对变量v的下标

image-20201124153547183

  1. LINE2：LHS中找到变量v
  2. LINE3：变量v的下标++
  3. LINE4：替换变量名
  4. LINE5-6：对RHS中用到的变量，加入def-use对集合DU中
  5. LINE7：将对v的定义加入Vdef中

对单条语句state的处理#

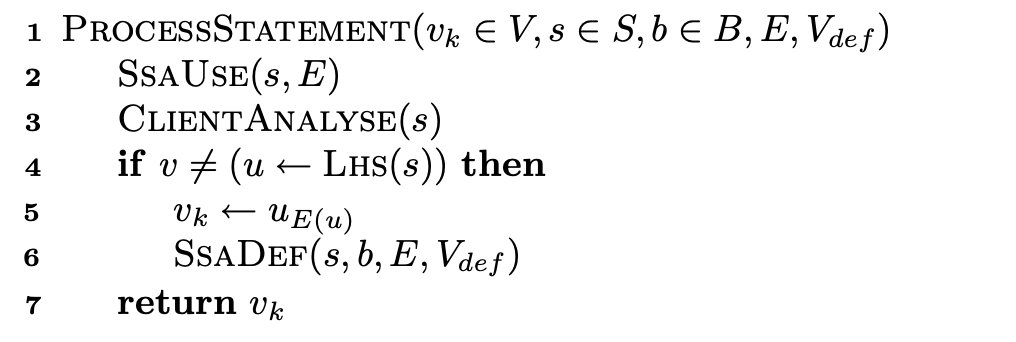
image-20201124153148061

  1. LINE2：找use点，改变量名
  2. LINE3：指针分析，后面会将具体的算法
  3. LINE4-6：找def点，改变量名

def传播和可达性传播#

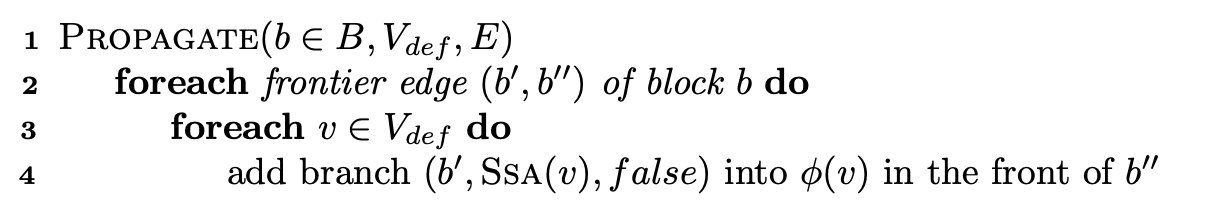
image-20201124153728459

image-20201124153737442

PROPAGATE会在基本块b的dominance frontiers引入PHI节点，并且设置该PHI节点为未访问状态

PropagateReachability是为了看当前块是否可以执行到该块的后继(无用分支)，当处理到后继节点时，会设置PHI节点为访问过的状态。

我感觉这两个函数可以理解为PHI节点会在dominator 节点引入，并且在dominated节点处理。

前向块分析#

根据引理2和引理3，实现前向块分析如下

image-20201124153138441

反向块分析#

根据引理4，实现反向块分析如下

image-20201124153824132

  1. LINE2：找包含回边的子图，将反向块变换成前向块
  2. LINE3：得到RPO序列
  3. LINE4-LINE6：按照前向块处理该子图

image-20201125160249077

image-20201125162150632

和IMSSA很像，只是不处理已经处理过的基本块

二进制优化框架#

框架试图通过正规化和删除无用代码，来缓解编译优化和混淆对相似代码检测的影响,由于框架是由指针分析驱动的，所以它应该对基于数据依赖的代码转换具有鲁棒性。

集成指针分析#

在实现IMSSA过程中，需要加入指针分析，除了E:V(Dominating def)和C:V(最大SSA下标数)，还需要维护D：V->E(变量->def表达式)和A:E->V（地址表达式->变量）

image-20201124161215234

  1. LINE 3-4：如果是变量，得到该变量的表达式
  2. LINE 5：遍历表达式中的变量，进行指针分析
  3. LINE 8：对分析后的语句进行归一化(逻辑)
  4. LINE 10-11：对指针变量进行处理

我们知道在IR中，STORE和LOAD都是对地址进行操作的，因此在实现指针分析时，主要关注这两个指令。

正规化和死代码删除#

正规化将等价但不同的表达式转换成统一形式，从而保持相似性。同时可以实现多级联合消除，例如公共子表达式消除等，进而去除无用代码

  • 正规化：收集了44个基本的消除规则(参考ollvm)，例如$(x \And c ) \oplus (x|c) \iff x \oplus c，(x \And c) |(x \And !c) \iff x$
  • 死代码删除：在根据def-use分析和可达性分析，删除无用代码

实现和评估#

作者在二进制分析平台BAP上以插件形式实现IMOPT过程：使用BAP将二进制转换到它的IR上BIR，然后用插件实现IMOPT过程

为了对比实验，也使用Mcsema将二进制转换到LLVM-IR上进行re-optimize(对比IMOPT优化和LLVM-OPT)的效果

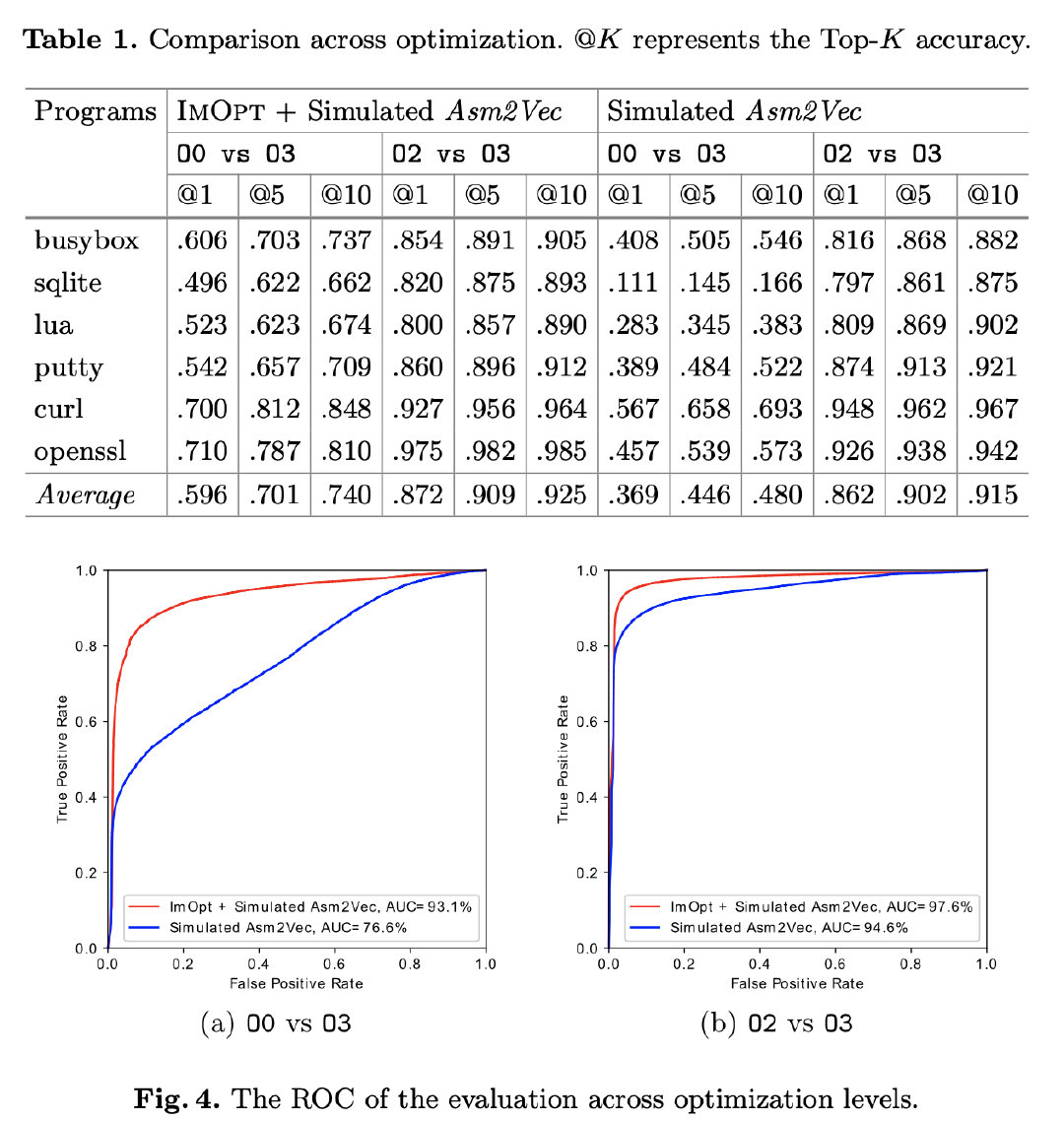
对比Asm2Vec#

1
2
3
4
5
 					BAP IR  ->   IMOPT  -> new binarys -> Asm2vec
        /                                                   \
binarys                                                       compare 
        \                                                   / 
           ------------------> Asm2vec -----------------

通过和Asm2Vec对比，IMOPT将准确率提高了近20%

image-20201124163336774

抗混淆性能#

ollvm回顾

-sub：指令混淆

image-20201125143529563

-bcf：引入虚假控制流：在原来的控制流图上，通过加入条件跳转语句跳转到一个原来的基本块或者是一个虚假的基本块，并最终跳转回条件跳转语句，引入循环结构，改变控制流图。

示例如下：

1
2
3
4
5
6
void f(int x){
	int i;
	for(i=0;i<x;i++){
	printf("%d",i);
	}
}

引入虚假控制流前

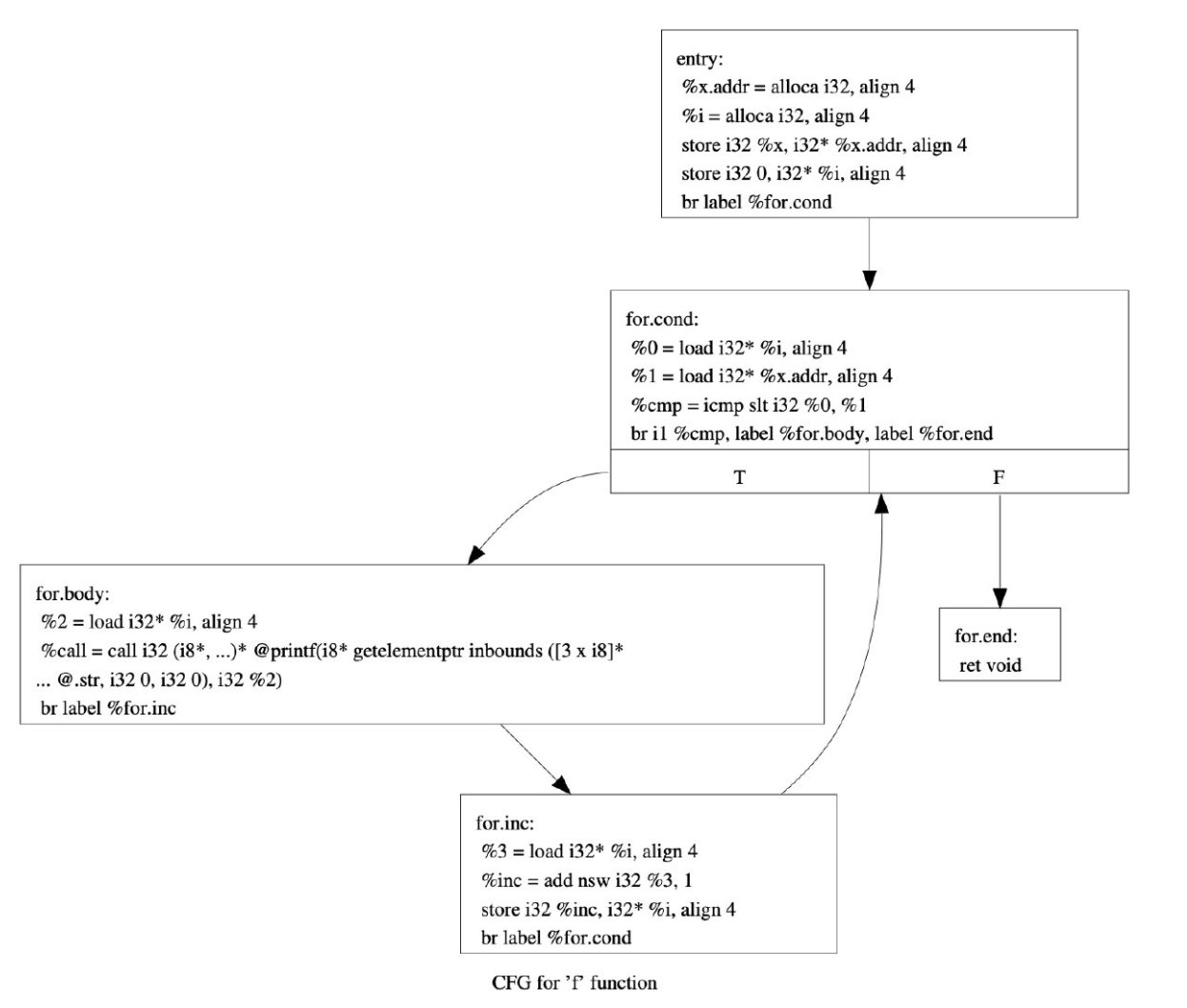
image-20201125145520337

引入虚假控制流后

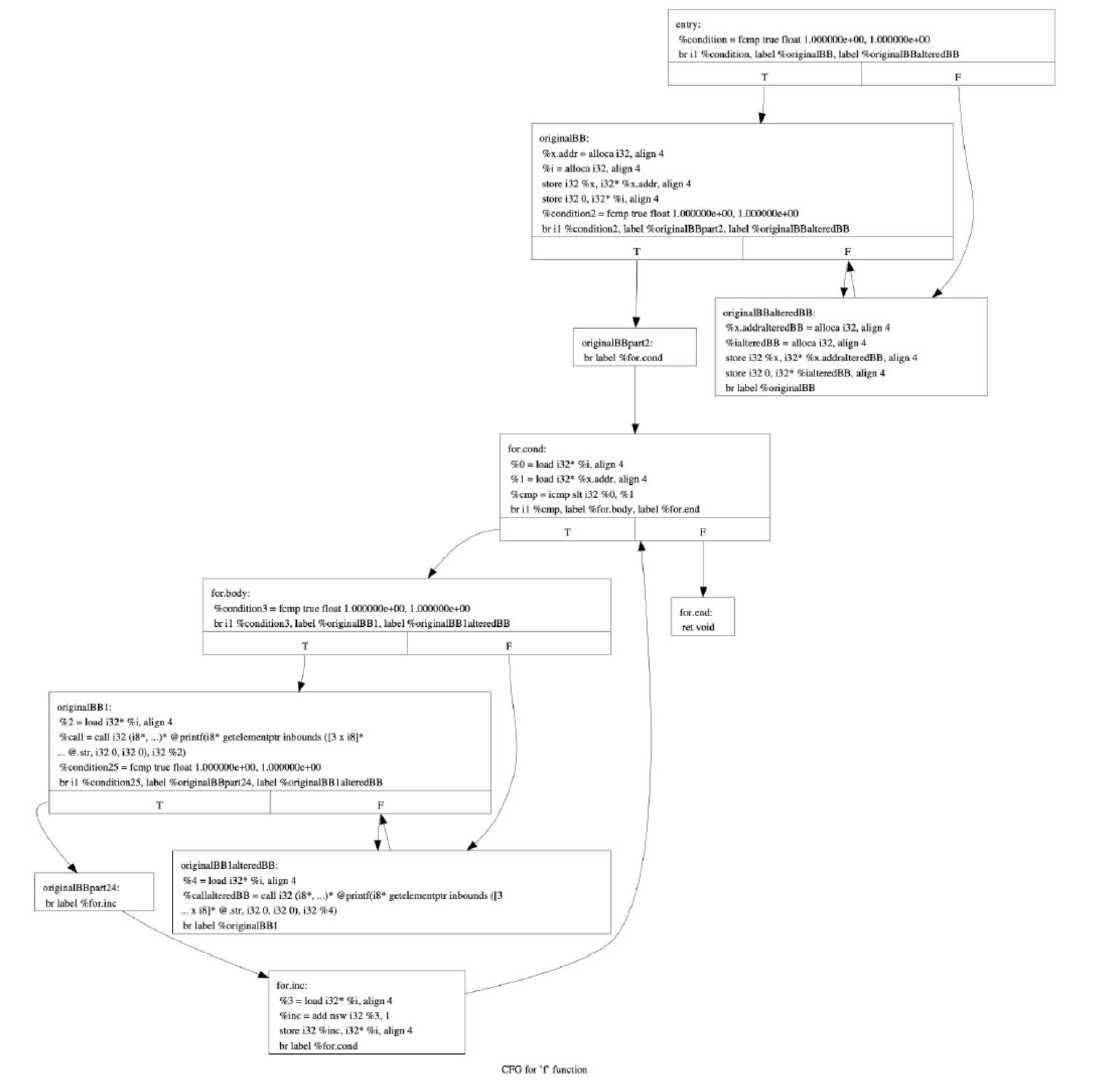
image-20201125145547632

-flat：控制流平坦化：使用一个主分发块，通过条件控制分别进入不同的基本块，然后再回到主分发块，虽然逻辑和原来的程序相同，但分析起来更加复杂，类似于虚拟机

对上面函数的控制流平坦化结果如下：

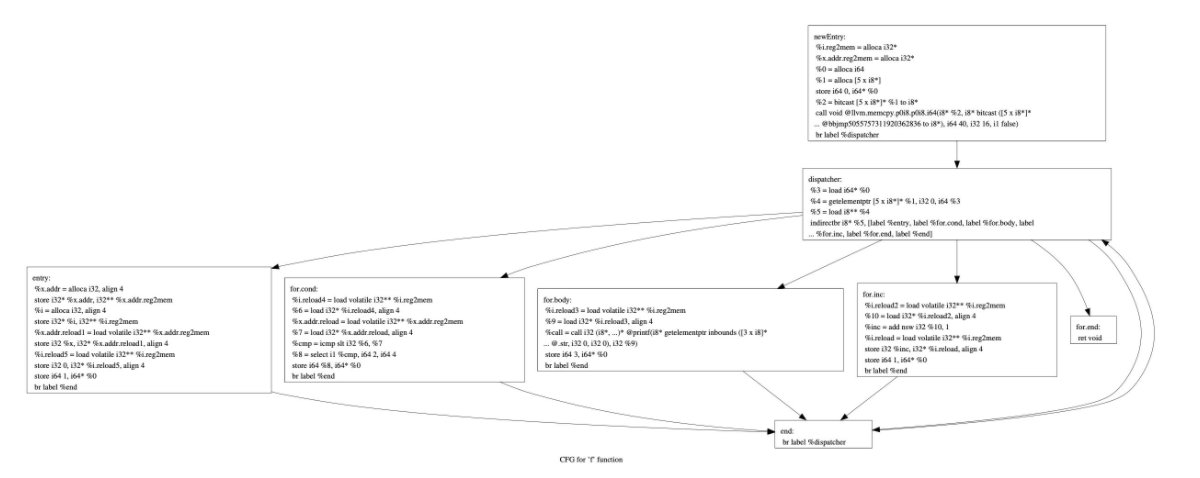
image-20201125145807147

使用ollvm 4.0混淆后进行测试，主要测试了-sub，-bcf，-flat选项，结果如下：

image-20201125145912158

1
2
3
4
5
 							   BAP IR  ->   IMOPT  -> new binarys -> Asm2vec
              /                                                   \
ollvm binarys                                                       compare 
              \                                                   / 
                LLVM IR  -> LLVM-OPT -> new binarys -> Asm2vec

指针分析效率对比#

和SDA(the most efficient approach that supports both pointer and reachability analysis)进行了比较，速度得到了大大提升(15.7x)。

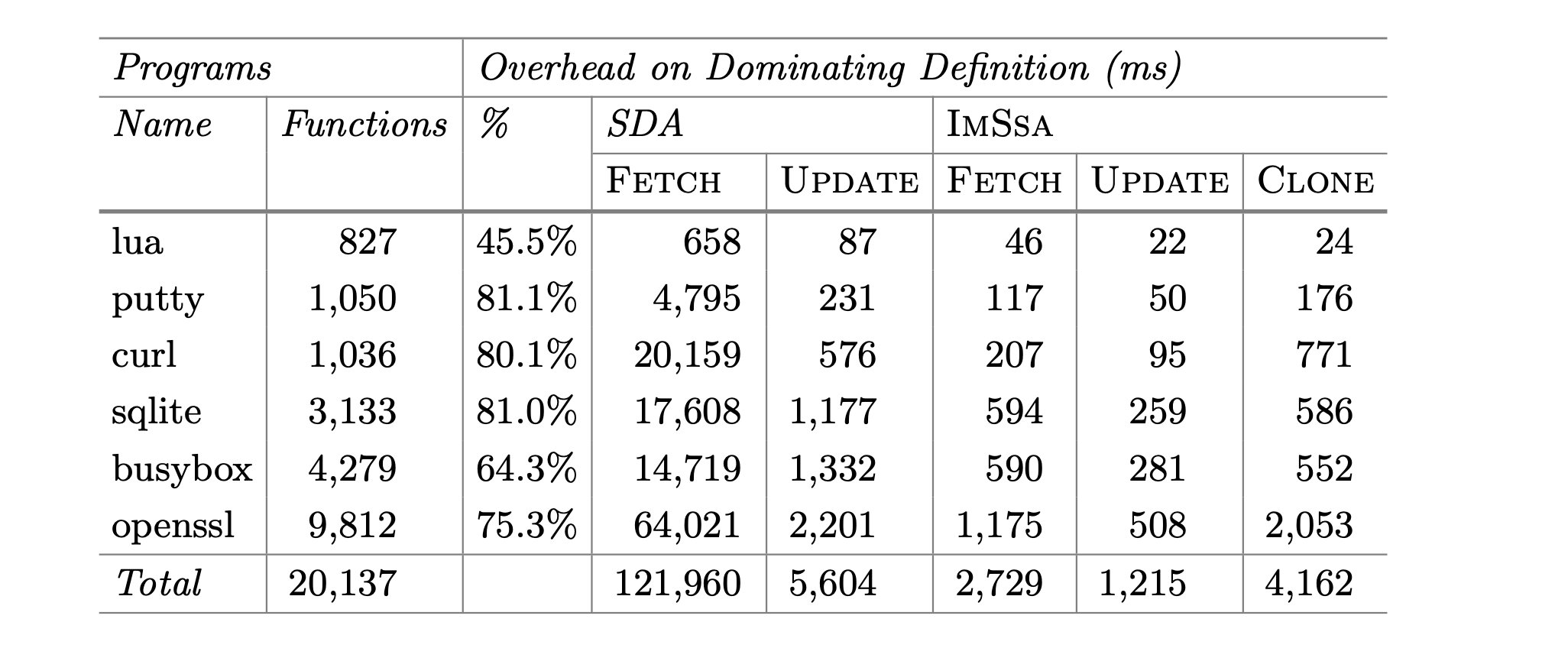
image-20201125162407166

总结#

我感觉这个东西虽然看起来艰涩难懂，但其实和传统的SSA算法区别没有很大，且对于最重要的指针分析作者并未提供十分有效的细节

另外有两个点值得去思考：

  1. 第一点：对于ollvm，有很多人做去混淆等相关工作了，看得出来这项工作有专门针对ollvm去做研究(比如复杂逻辑的缩减)，不知道对于其他的混淆方法，效果是否有对ollvm的提升那么明显
  2. 第二点是我自己也不明白的，文中指出即使是编译器对指针分析后优化也会出错，但从算法上看或者也没有案例说明文中的算法不会出现类似的问题

参考资料#

#

喜欢这篇文章？打赏一下作者吧

评论

关注我

链接

归档

订阅更新

邮件订阅，更新早知道

分类

最新文章

标签

AI2
CTF48
CVE4
Fuzz1
FuzzingBook1
HEVD5
NLP1
PyQt512
ROP Emporium2
Toddler's Bottle21
Web1
automatic analyse10
binary analyse1
codeql5
crypto7
fuzz3
life2
linux kernel2
machine learning1
mobile security1
others1
paper18
pentest3
pwn24
pwnable.kr21
re5
research20
security18
security situation awareness2
stack overflow3
tools2
windows8
work1
writeup5
数据库11
×